Skip to contents

Seawater Potential Temperature (UNESCO Version)

Source: R/sw.R
swTheta.Rd

Compute the potential temperature of seawater, denoted \(\theta\) in the UNESCO system, and pt in the GSW system.

Usage

swTheta(
  salinity,
  temperature = NULL,
  pressure = NULL,
  referencePressure = 0,
  longitude = NULL,
  latitude = NULL,
  eos = getOption("oceEOS", default = "gsw"),
  debug = getOption("oceDebug")
)

Arguments

salinity

either salinity (PSU) (in which case temperature and pressure must be provided) or an oce object (in which case salinity, etc. are inferred from the object).

temperature

in-situ temperature (\(^\circ\)C), defined on the ITS-90 scale; see “Temperature units” in the documentation for swRho(), and the examples below.

pressure

pressure (dbar)

referencePressure

reference pressure (dbar)

longitude

longitude of observation (only used if eos="gsw"; see “Details”).

latitude

latitude of observation (only used if eos="gsw"; see “Details”).

eos

equation of state, either "unesco" (references 1 and 2) or "gsw" (references 3 and 4).

debug

an integer specifying whether debugging information is to be printed during the processing. This is a general parameter that is used by many oce functions. Generally, setting debug=0 turns off the printing, while higher values suggest that more information be printed. If one function calls another, it usually reduces the value of debug first, so that a user can often obtain deeper debugging by specifying higher debug values.

Value

Potential temperature (\(^\circ\)C) of seawater, referenced to pressure referencePressure.

Details

Different formulae are used depending on the equation of state. If eos is "unesco", the method of Fofonoff et al. (1983) is used (see references 1 and 2). Otherwise, swTheta uses gsw::gsw_pt_from_t() from the gsw package.

If the first argument is a ctd or section object, then values for salinity, etc., are extracted from it, and used for the calculation, and the corresponding arguments to the present function are ignored.

References

  1. Fofonoff, P. and R. C. Millard Jr, 1983. Algorithms for computation of fundamental properties of seawater. Unesco Technical Papers in Marine Science, 44, 53 pp

  2. Gill, A.E., 1982. Atmosphere-ocean Dynamics, Academic Press, New York, 662 pp.

  3. IOC, SCOR, and IAPSO (2010). The international thermodynamic equation of seawater-2010: Calculation and use of thermodynamic properties. Technical Report 56, Intergovernmental Oceanographic Commission, Manuals and Guide.

  4. McDougall, T.J. and P.M. Barker, 2011: Getting started with TEOS-10 and the Gibbs Seawater (GSW) Oceanographic Toolbox, 28pp., SCOR/IAPSO WG127, ISBN 978-0-646-55621-5.

See also

Other functions that calculate seawater properties: T68fromT90(), T90fromT48(), T90fromT68(), computableWaterProperties(), locationForGsw(), swAbsoluteSalinity(), swAlpha(), swAlphaOverBeta(), swBeta(), swCSTp(), swConservativeTemperature(), swDepth(), swDynamicHeight(), swLapseRate(), swN2(), swPressure(), swRho(), swRrho(), swSCTp(), swSR(), swSTrho(), swSigma(), swSigma0(), swSigma1(), swSigma2(), swSigma3(), swSigma4(), swSigmaT(), swSigmaTheta(), swSoundAbsorption(), swSoundSpeed(), swSpecificHeat(), swSpice(), swSpiciness0(), swSpiciness1(), swSpiciness2(), swSstar(), swTFreeze(), swTSrho(), swThermalConductivity(), swViscosity(), swZ()

Author

Dan Kelley

Examples

library(oce)
# Example 1: test value from Fofonoff et al., 1983
stopifnot(abs(36.8818748026 - swTheta(40, T90fromT68(40), 10000, 0, eos = "unesco")) < 0.0000000001)

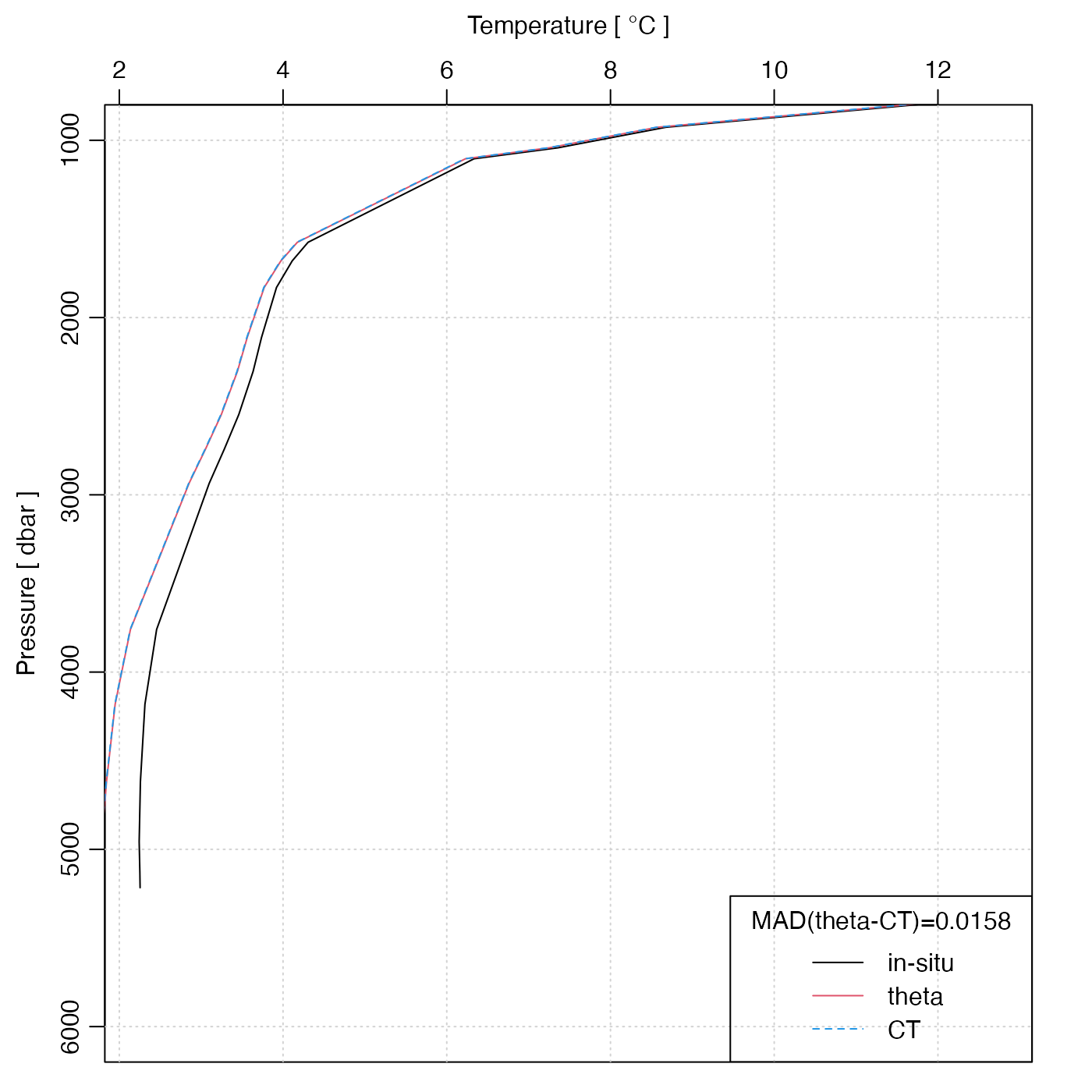
# Example 2: a deep-water station. Note that theta and CT are
# visually identical on this scale.
data(section)
stn <- section[["station", 70]]
plotProfile(stn, "temperature", ylim = c(6000, 1000))
lines(stn[["theta"]], stn[["pressure"]], col = 2)
lines(stn[["CT"]], stn[["pressure"]], col = 4, lty = 2)
legend("bottomright",
    lwd = 1, col = c(1, 2, 4), lty = c(1, 1, 2),
    legend = c("in-situ", "theta", "CT"),
    title = sprintf("MAD(theta-CT)=%.4f", mean(abs(stn[["theta"]] - stn[["CT"]])))
)