Skip to contents

Seawater Freezing Temperature

Source: R/sw.R
swTFreeze.Rd

Compute in-situ freezing temperature of seawater, using either the UNESCO formulation (computed as in Section 5 of Fofonoff and Millard, 1983) or the GSW formulation (computed by using gsw::gsw_SA_from_SP() to get Absolute Salinity, and then gsw::gsw_t_freezing() to get the freezing temperature).

Usage

swTFreeze(
  salinity,
  pressure = NULL,
  longitude = NULL,
  latitude = NULL,
  saturation_fraction = 1,
  eos = getOption("oceEOS", default = "gsw")
)

Arguments

salinity

Either practical salinity (PSU) or a ctd object from which practical salinity and pressure (plus in the eos="gsw" case, longitude and latitude) are inferred.

pressure

Seawater pressure (dbar).

longitude

Longitude of observation (only used if eos="gsw"; see “Details”).

latitude

Latitude of observation (only used if eos="gsw"; see “Details”).

saturation_fraction

The saturation fraction of dissolved air in seawater, ignored if eos="unesco").

eos

The equation of state, either "unesco" (Fofonoff and Millard, 1983; Gill 1982) or "gsw" (IOC, SCOR and IAPSO 2010; McDougall and Barker 2011).

Value

Temperature (degC), defined on the ITS-90 scale.

Details

If the first argument is an oce object, and if the pressure argument is NULL, then the pressure is sought within the first argument. In the case of eos="gsw", then a similar procedure also applies to the longitude and latitude arguments.

References

Fofonoff, N. P., and R. C. Millard. Algorithms for Computation of Fundamental Properties of Seawater. UNESCO Technical Papers in Marine Research. SCOR working group on Evaluation of CTD data; UNESCO/ICES/SCOR/IAPSO Joint Panel on Oceanographic Tables and Standards, 1983.

Gill, A E. Atmosphere-Ocean Dynamics. New York, NY, USA: Academic Press, 1982.

IOC, SCOR, and IAPSO (2010). The international thermodynamic equation of seawater-2010: Calculation and use of thermodynamic properties. Technical Report 56, Intergovernmental Oceanographic Commission, Manuals and Guide, 2010.

McDougall, Trevor J., and Paul M. Barker. Getting Started with TEOS-10 and the Gibbs Seawater (GSW) Oceanographic Toolbox. SCOR/IAPSO WG127, 2011.

See also

Other functions that calculate seawater properties: T68fromT90(), T90fromT48(), T90fromT68(), computableWaterProperties(), locationForGsw(), swAbsoluteSalinity(), swAlpha(), swAlphaOverBeta(), swBeta(), swCSTp(), swConservativeTemperature(), swDepth(), swDynamicHeight(), swLapseRate(), swN2(), swPressure(), swRho(), swRrho(), swSCTp(), swSR(), swSTrho(), swSigma(), swSigma0(), swSigma1(), swSigma2(), swSigma3(), swSigma4(), swSigmaT(), swSigmaTheta(), swSoundAbsorption(), swSoundSpeed(), swSpecificHeat(), swSpice(), swSpiciness0(), swSpiciness1(), swSpiciness2(), swSstar(), swTSrho(), swThermalConductivity(), swTheta(), swViscosity(), swZ()

Author

Dan Kelley

Examples

# 1. Test for a check-value given in reference 1. This value, -2.588567 degC,
# is in the 1968 temperature scale (IPTS-68), but swTFreeze reports
# in the newer ITS-90 scale, so we must convert before checking.
Tcheck <- -2.588567 # IPTS-68
T <- swTFreeze(salinity = 40, pressure = 500, eos = "unesco")
stopifnot(abs(Tcheck - T68fromT90(T)) < 1e-6)

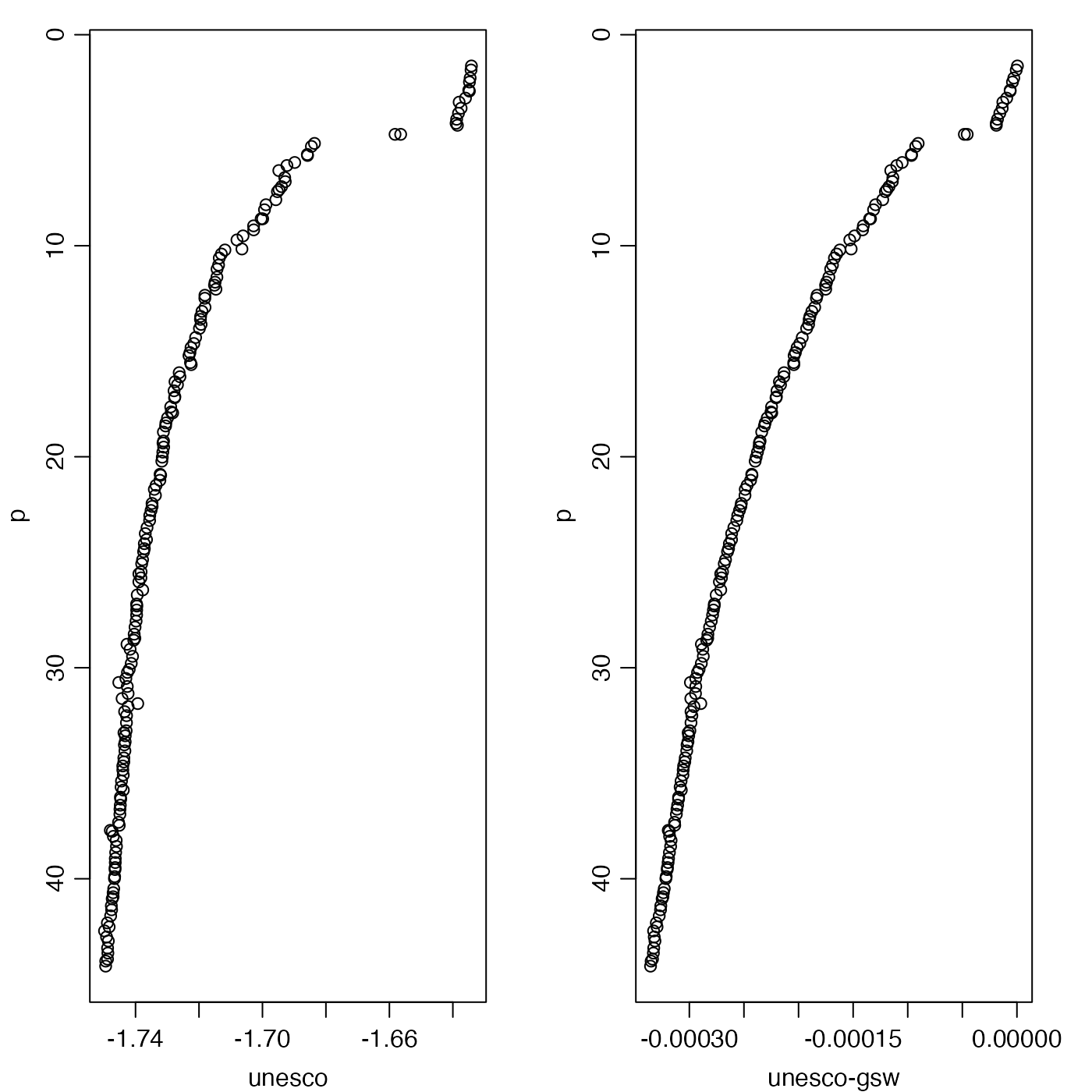
# 2. Compare unesco and gsw formulations.
data(ctd)
p <- ctd[["pressure"]]
par(mfrow = c(1, 2), mar = c(3, 3, 1, 2), mgp = c(2, 0.7, 0))
plot(swTFreeze(ctd, eos = "unesco"),
    p,
    xlab = "unesco", ylim = rev(range(p))
)
plot(swTFreeze(ctd, eos = "unesco") - swTFreeze(ctd, eos = "gsw"),
    p,
    xlab = "unesco-gsw", ylim = rev(range(p))
)