Squared Buoyancy Frequency for Seawater

Compute \(N^2\), the square of the buoyancy frequency for a seawater profile.

Usage

swN2(
  pressure,
  sigmaTheta = NULL,
  derivs,
  df,
  debug = getOption("oceDebug"),
  ...
)

Arguments

pressure: either pressure (dbar) (in which case sigmaTheta must be provided) or an object of class ctd object (in which case sigmaTheta is inferred from the object.
sigmaTheta: Surface-referenced potential density minus 1000 (kg/m\(^3\)).
derivs: optional argument to control how the derivative \(d\sigma_\theta/dp\) is calculated. This may be a character string or a function of two arguments. See “Details”.
df: argument passed to smooth.spline() if this function is used for smoothing; set to NA to prevent smoothing.
debug: an integer specifying whether debugging information is to be printed during the processing. This is a general parameter that is used by many oce functions. Generally, setting debug=0 turns off the printing, while higher values suggest that more information be printed. If one function calls another, it usually reduces the value of debug first, so that a user can often obtain deeper debugging by specifying higher debug values.
...: additional argument, passed to smooth.spline(), in the case that derivs="smoothing". See “Details”.

Value

Square of buoyancy frequency (\(radian^2/s^2\)).

Details

Smoothing is often useful prior to computing buoyancy frequency, and so this may optionally be done with smooth.spline(), unless df=NA, in which case raw data are used. If df is not provided, a possibly reasonable value computed from an analysis of the profile, based on the number of pressure levels.

The core of the method involves computing potential density referenced to median pressure, using the UNESCO-style swSigmaTheta function, and then differentiating this with respect to pressure. The derivs argument is used to control how this is done, as follows.

If derivs is not supplied, the action is as though it were given as the string "smoothing"
If derivs equals "simple", then the derivative of density with respect to pressure is calculated as the ratio of first-order derivatives of density and pressure, each calculated using diff(). (A zero is appended at the top level.)
If derivs equals "smoothing", then the processing depends on the number of data in the profile, and on whether df is given as an optional argument. When the number of points exceeds 4, and when df exceeds 1, smooth.spline() is used to calculate smoothing spline representation the variation of density as a function of pressure, and derivatives are extracted from the spline using predict. Otherwise, density is smoothed using smooth(), and derivatives are calculated as with the "simple" method.
If derivs is a function taking two arguments (first pressure, then density) then that function is called directly to calculate the derivative, and no smoothing is done before or after that call.

For precise work, it makes sense to skip swN2 entirely, choosing whether, what, and how to smooth based on an understanding of fundamental principles as well as data practicalities.

Deprecation Notice

Until 2019 April 11, swN2 had an argument named eos. However, this did not work as stated, unless the first argument was a ctd object. Besides, the argument name was inherently deceptive, because the UNESCO scheme does not specify how N2 is to be calculated. Nothing is really lost by making this change, because the new default is the same as was previously available with the eos="unesco" setup, and the gsw-formulated estimate of N2 is provided by gsw::gsw_Nsquared() in the gsw package.

The gsw::gsw_Nsquared() function of the gsw provides an alternative to this, as formulated in the GSW system. It has a more sophisticated treatment of potential density, but it is based on simple first-difference derivatives, so its results may require smoothing, depending on the dataset and purpose of the analysis.

Other functions that calculate seawater properties: T68fromT90(), T90fromT48(), T90fromT68(), computableWaterProperties(), locationForGsw(), swAbsoluteSalinity(), swAlpha(), swAlphaOverBeta(), swBeta(), swCSTp(), swConservativeTemperature(), swDepth(), swDynamicHeight(), swLapseRate(), swPressure(), swRho(), swRrho(), swSCTp(), swSR(), swSTrho(), swSigma(), swSigma0(), swSigma1(), swSigma2(), swSigma3(), swSigma4(), swSigmaT(), swSigmaTheta(), swSoundAbsorption(), swSoundSpeed(), swSpecificHeat(), swSpice(), swSpiciness0(), swSpiciness1(), swSpiciness2(), swSstar(), swTFreeze(), swTSrho(), swThermalConductivity(), swTheta(), swViscosity(), swZ()

Author

Dan Kelley

Examples


library(oce)
data(ctd)
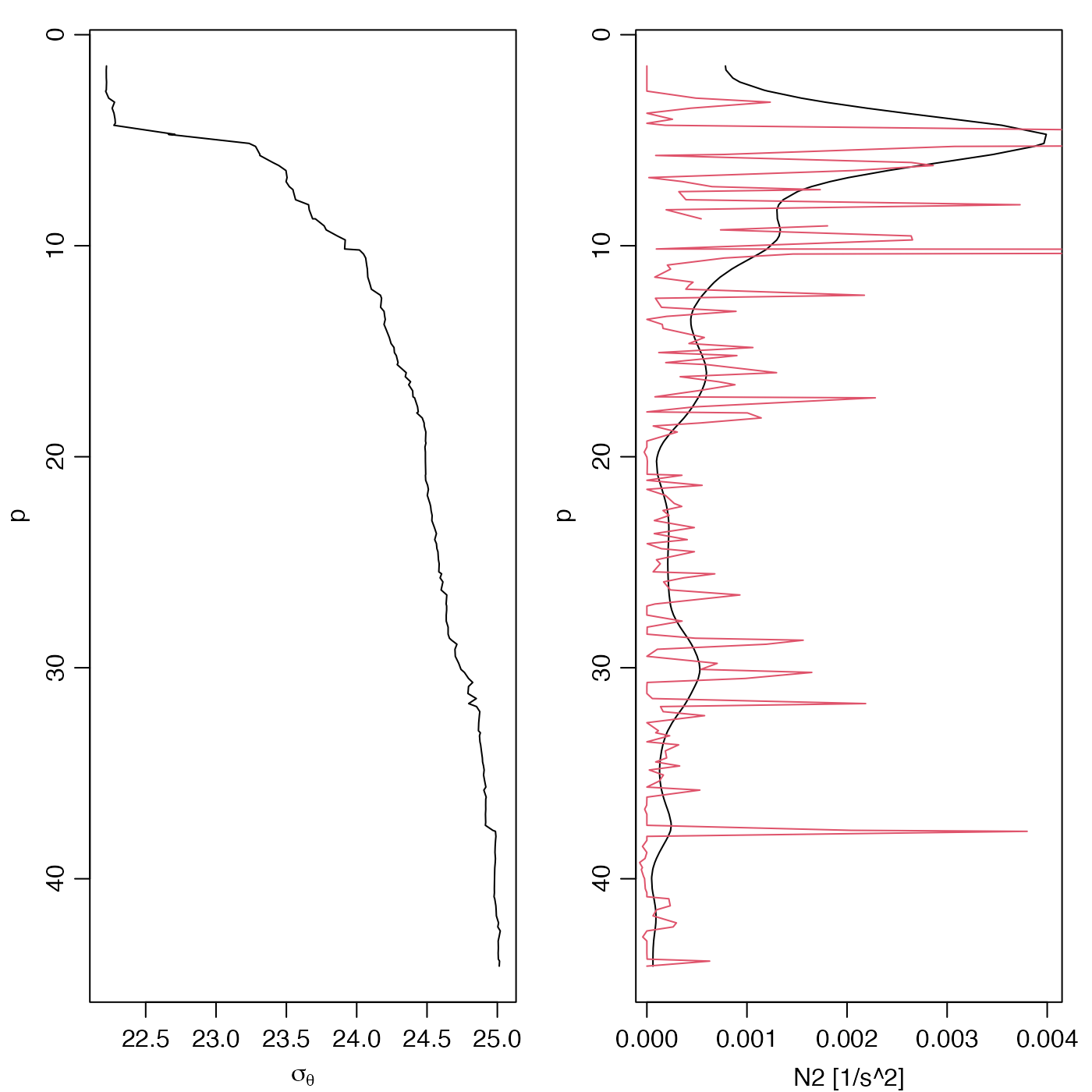
# Left panel: density
p <- ctd[["pressure"]]
ylim <- rev(range(p))
par(mfrow = c(1, 2), mar = c(3, 3, 1, 1), mgp = c(2, 0.7, 0))
plot(ctd[["sigmaTheta"]], p, ylim = ylim, type = "l", xlab = expression(sigma[theta]))
# Right panel: N2, with default settings (black) and with df=2 (red)
N2 <- swN2(ctd)
plot(N2, p, ylim = ylim, xlab = "N2 [1/s^2]", ylab = "p", type = "l")
lines(swN2(ctd, df = 3), p, col = 2)