Lunar Angle as Function of Space and Time

Source: R/moon.R

The calculations are based on formulae provided by Meeus (1982), primarily in chapters 6, 18, and 30. The first step is to compute sidereal time as formulated in Meeus (1982) chapter 7, which in turn uses Julian day computed according to as formulae in Meeus (1982) chapter 3. Using these quantities, formulae in Meeus (1982) chapter 30 are then used to compute geocentric longitude (\(lambda\), in the Meeus notation), geocentric latitude (\(beta\)), and parallax. Then the obliquity of the ecliptic is computed with Meeus (1982) equation 18.4. Equatorial coordinates (right ascension and declination) are computed with equations 8.3 and 8.4 from Meeus (1982), using eclipticalToEquatorial(). The hour angle (\(H\)) is computed using the unnumbered equation preceding Meeus's (1982) equation 8.1. 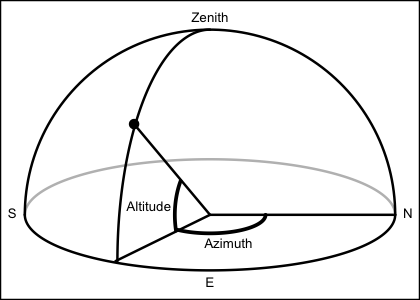Finally, Meeus (1982) equations 8.5 and 8.6 are used to calculate the local azimuth and altitude of the moon, using equatorialToLocalHorizontal().

moonAngle(t, longitude = 0, latitude = 0, useRefraction = TRUE)

Arguments

t

time, a POSIXt object (converted to timezone "UTC", if it is not already in that timezone), a character or numeric value that corresponds to such a time.

longitude

observer longitude in degrees east

latitude

observer latitude in degrees north

useRefraction

boolean, set to TRUE to apply a correction for atmospheric refraction. (Ignored at present.)

Value

A list containing the following.

  • time

  • azimuth moon azimuth, in degrees eastward of north, from 0 to 360. Note: this is not the convention used by Meeus, who uses degrees westward of South. Here, the convention is chosen to more closely match the expectation of oceanographers.

  • altitude moon altitude, in degrees from -90 to 90.

  • rightAscension in' degrees.

  • declination in degrees.

  • lambda geocentric longitude, in degrees.

  • beta geocentric latitude, in degrees.

  • diameter lunar diameter, in degrees.

  • distance earth-moon distance, in kilometers.

  • illuminatedFraction fraction of moon's visible disk that is illuminated.

  • phase phase of the moon, defined in equation 32.3 of Meeus (1982). The fractional part of which is 0 for new moon, 1/4 for first quarter, 1/2 for full moon, and 3/4 for last quarter.

Alternate formulations

Formulae provide by Meeus (1982) are used for all calculations here. Meeus (1991) provides formulae that are similar, but that differ in the 5th or 6th digits. For example, the formula for ephemeris time in Meeus (1991) differs from that in Meeus (1992) at the 5th digit, and almost all of the approximately 200 coefficients in the relevant formulae also differ in the 5th and 6th digits. Discussion of the changing formulations is best left to members of the astronomical community. For the present purpose, it may be sufficient to note that moonAngle, based on Meeus (1982), reproduces the values provided in example 45.a of Meeus (1991) to 4 significant digits, e.g. with all angles matching to under 2 minutes of arc.

References

  • Meeus, Jean. Astronomical Formulas for Calculators. Second Edition. Richmond, Virginia, USA: Willmann-Bell, 1982.

  • Meeus, Jean. Astronomical Algorithms. Second Edition. Richmond, Virginia, USA: Willmann-Bell, 1991.

See also

The equivalent function for the sun is sunAngle().

Other things related to astronomy: angle2hms(), eclipticalToEquatorial(), equatorialToLocalHorizontal(), julianCenturyAnomaly(), julianDay(), siderealTime(), sunAngle(), sunDeclinationRightAscension()

Author

Dan Kelley, based on formulae in Meeus (1982).

Examples


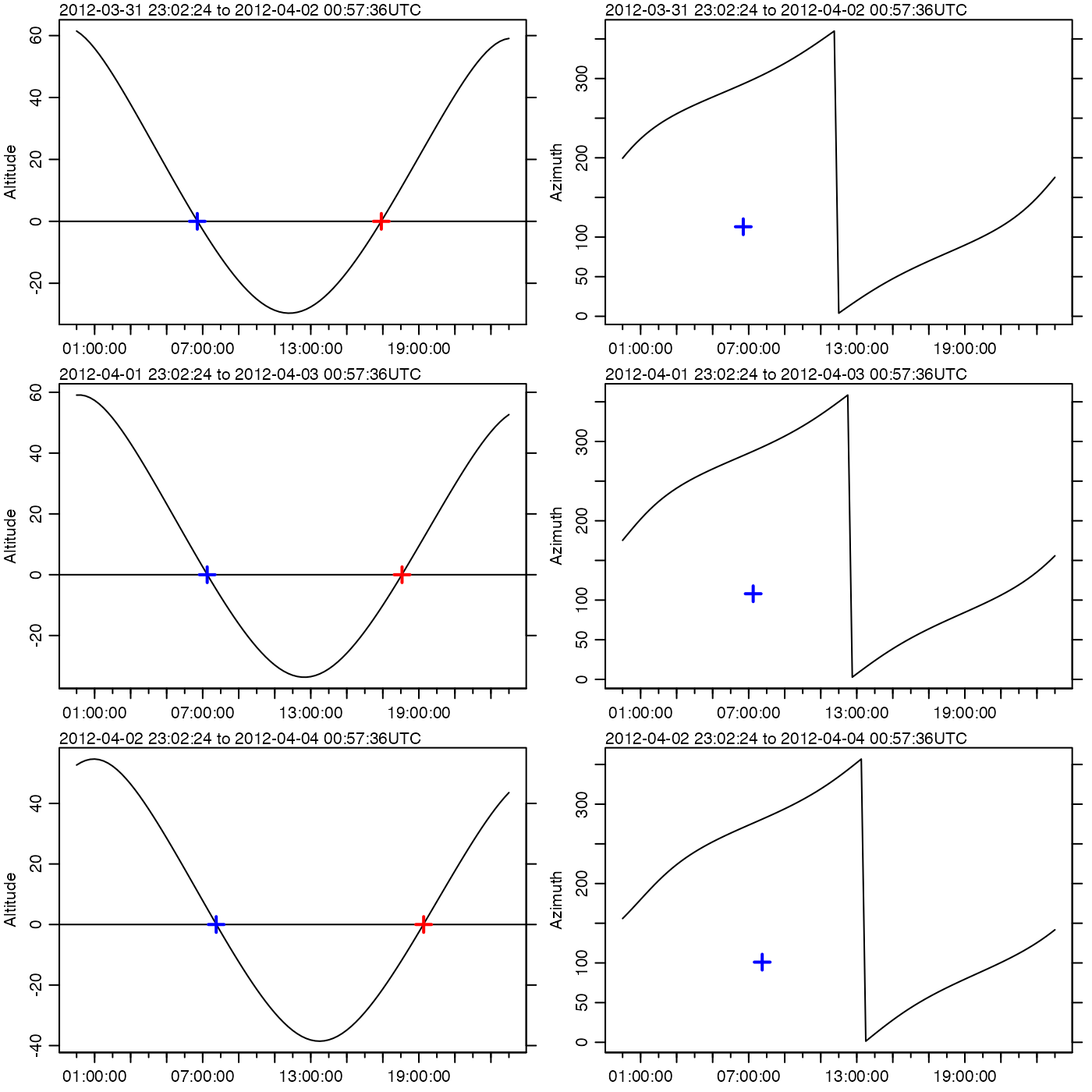
library(oce)
par(mfrow = c(3, 2))
y <- 2012
m <- 4
days <- 1:3
# Halifax sunrise/sunset (see e.g. https://www.timeanddate.com/worldclock)
rises <- ISOdatetime(y, m, days, c(13, 15, 16), c(55, 04, 16), 0, tz = "UTC") + 3 * 3600 # ADT
sets <- ISOdatetime(y, m, days, c(3, 4, 4), c(42, 15, 45), 0, tz = "UTC") + 3 * 3600
azrises <- c(69, 75, 82)
azsets <- c(293, 288, 281)
latitude <- 44.65
longitude <- -63.6
for (i in 1:3) {
    t <- ISOdatetime(y, m, days[i], 0, 0, 0, tz = "UTC") + seq(0, 24 * 3600, 3600 / 4)
    ma <- moonAngle(t, longitude, latitude)
    oce.plot.ts(t, ma$altitude, type = "l", mar = c(2, 3, 1, 1), cex = 1 / 2, ylab = "Altitude")
    abline(h = 0)
    points(rises[i], 0, col = "red", pch = 3, lwd = 2, cex = 1.5)
    points(sets[i], 0, col = "blue", pch = 3, lwd = 2, cex = 1.5)
    oce.plot.ts(t, ma$azimuth, type = "l", mar = c(2, 3, 1, 1), cex = 1 / 2, ylab = "Azimuth")
    points(rises[i], -180 + azrises[i], col = "red", pch = 3, lwd = 2, cex = 1.5)
    points(sets[i], -180 + azsets[i], col = "blue", pch = 3, lwd = 2, cex = 1.5)
}