Skip to contents

Solar Angle as Function of Space and Time

Source: R/sun.R
sunAngle.Rd

This calculates solar angle, based on a NASA-provided Fortran program, which (according to comments in the code) is in turn based on "The Astronomical Almanac". Note that time may be a single value or a vector of values; in the latter case, longitude, latitude and useRefraction are all made to be of the same length as time, by calling rep(). This addresses the case of finding a time-series of angles at a given spatial location. For other cases of arguments that are not single values, either call sunAngle() repeatedly or, if that is too slow, use expand.grid() to set up values of uniform length that are then supplied to sunAngle().

Usage

sunAngle(t, longitude = 0, latitude = 0, useRefraction = FALSE)

Arguments

t

time, either a POSIXt object (converted to timezone "UTC", if it is not already in that timezone), or a value (character or numeric) that can be converted to a time with as.POSIXct(), assuming the timezone to be "UTC".

longitude

observer longitude in degrees east.

latitude

observer latitude in degrees north.

useRefraction

boolean, set to TRUE to apply a correction for atmospheric refraction.

Value

A list containing the following:

  • time the time

  • azimuth, in degrees eastward of north, from 0 to 360.

  • altitude, in degrees above the horizon, ranging from -90 to 90.

  • diameter, solar diameter, in degrees.

  • distance to sun, in astronomical units.

  • declination angle in degrees, computed with sunDeclinationRightAscension().

  • rightAscension angle in degrees, computed with sunDeclinationRightAscension().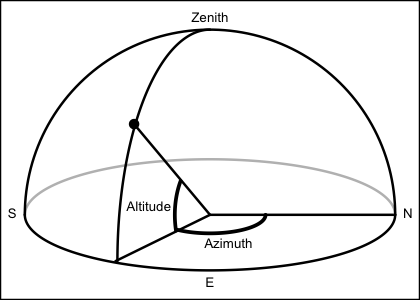

References

Regarding declination and rightAscension, see references in the documentation for sunDeclinationRightAscension(). The other items are based on Fortran code retrieved from the file sunae.f, downloaded from the ftp site climate1.gsfc.nasa.gov/wiscombe/Solar_Rad/SunAngles on 2009-11-1. Comments in that code list as references:

Michalsky, J., 1988: The Astronomical Almanac's algorithm for approximate solar position (1950-2050), Solar Energy 40, 227-235

The Astronomical Almanac, U.S. Gov't Printing Office, Washington, D.C. (published every year).

The code comments suggest that the appendix in Michalsky (1988) contains errors, and declares the use of the following formulae in the 1995 version the Almanac:

  • p. A12: approximation to sunrise/set times

  • p. B61: solar altitude (AKA elevation) and azimuth

  • p. B62: refraction correction

  • p. C24: mean longitude, mean anomaly, ecliptic longitude, obliquity of ecliptic, right ascension, declination, Earth-Sun distance, angular diameter of Sun

  • p. L2: Greenwich mean sidereal time (ignoring T^2, T^3 terms)

The code lists authors as Dr. Joe Michalsky and Dr. Lee Harrison (State University of New York), with modifications by Dr. Warren Wiscombe (NASA Goddard Space Flight Center).

See also

The corresponding function for the moon is moonAngle().

Other things related to astronomy: angle2hms(), eclipticalToEquatorial(), equatorialToLocalHorizontal(), julianCenturyAnomaly(), julianDay(), moonAngle(), siderealTime(), sunDeclinationRightAscension()

Author

Dan Kelley

Examples


rise <- as.POSIXct("2011-03-03 06:49:00", tz = "UTC") + 4 * 3600
set <- as.POSIXct("2011-03-03 18:04:00", tz = "UTC") + 4 * 3600
mismatch <- function(lonlat) {
    sunAngle(rise, lonlat[1], lonlat[2])$altitude^2 + sunAngle(set, lonlat[1], lonlat[2])$altitude^2
}
result <- optim(c(1, 1), mismatch)
lonHfx <- (-63.55274)
latHfx <- 44.65
dist <- geodDist(result$par[1], result$par[2], lonHfx, latHfx)
cat(sprintf(
    "Infer Halifax latitude %.2f and longitude %.2f; distance mismatch %.0f km",
    result$par[2], result$par[1], dist
))
#> Infer Halifax latitude 39.44 and longitude -63.56; distance mismatch 579 km