Convert From Geographical to Geodesic Coordinates

The method, which may be useful in determining coordinate systems for a mooring array or a ship transects, calculates (x,y) from distance calculations along geodesic curves. See “Caution”.

Usage

geodXy(
  longitude,
  latitude,
  longitudeRef,
  latitudeRef,
  debug = getOption("oceDebug")
)

Arguments

longitude, latitude

vector of longitude and latitude

longitudeRef, latitudeRef

numeric reference location. Poor results will be returned if these values are not close to the locations described by longitude and latitude. A sensible approach might be to set longitudeRef to longitude[1], etc.

debug

an integer specifying whether debugging information is to be printed during the processing. This is a general parameter that is used by many oce functions. Generally, setting debug=0 turns off the printing, while higher values suggest that more information be printed. If one function calls another, it usually reduces the value of debug first, so that a user can often obtain deeper debugging by specifying higher debug values.

Value

geodXy returns a data frame of x and y, geodesic distance components, measured in metres.

Details

The calculation is as follows. Consider the i-th point in the longitude and latitude vectors. To calculate x[i], geodDist() is used is to find the distance along a geodesic curve connecting (longitude[i], latitude[i]) with (longitudeRef, latitude[i]). The resultant distance is multiplied by -1 if longitude[i]-longitudeRef is negative, and the result is assigned to x[i]. A similar procedure is used for y[i].

Caution

This scheme is without known precedent in the literature, and users should read the documentation carefully before deciding to use it.

Change history

On 2015-11-02, the names of the arguments were changed from lon, etc., to longitude, etc., to be in keeping with other oce functions.

On 2017-04-05, four changes were made.

1. Default values of longitudeRef and latitudeRef were removed, since the old defaults were inappropriate to most work.

2. The argument called rotate was eliminated, because it only made sense if the mean resultant x and y were zero.

3. The example was made more useful.

4. Pointers were made to lonlat2utm(), which may be more useful.

See also

geodDist()

Other functions relating to geodesy: geodDist(), geodGc(), geodXyInverse()

Author

Dan Kelley

Examples

# \donttest{
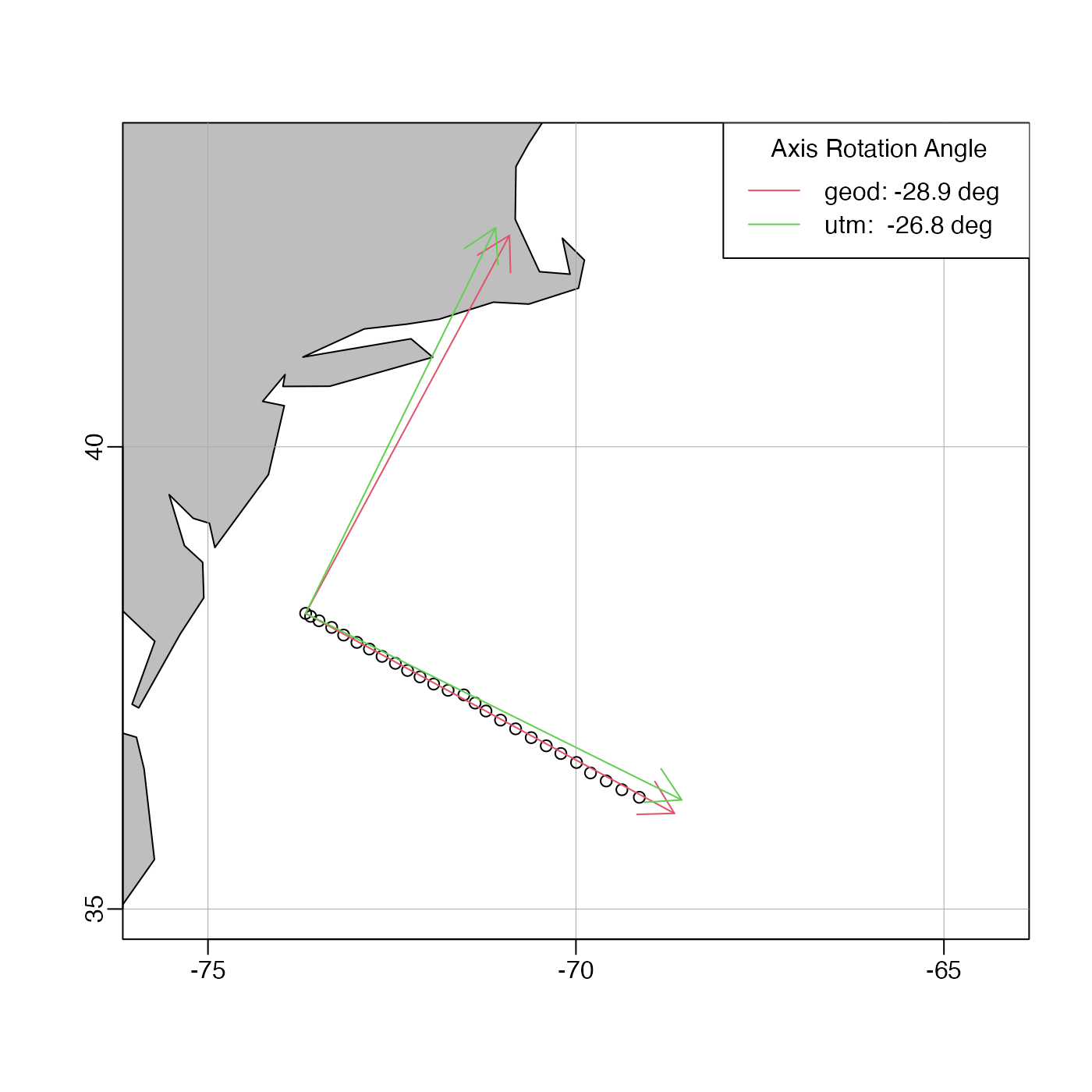
# Develop a transect-based axis system for final data(section) stations
library(oce)
data(section)
lon <- tail(section[["longitude", "byStation"]], 26)
lat <- tail(section[["latitude", "byStation"]], 26)
lonR <- tail(lon, 1)
latR <- tail(lat, 1)
data(coastlineWorld)
mapPlot(coastlineWorld,
    projection = "+proj=merc",
    longitudelim = c(-75, -65), latitudelim = c(35, 43), col = "gray"
)
mapPoints(lon, lat)
XY <- geodXy(lon, lat, mean(lon), mean(lat))
angle <- 180 / pi * atan(coef(lm(y ~ x, data = XY))[2])
mapCoordinateSystem(lonR, latR, 500, angle, col = 2)
# Compare UTM calculation
UTM <- lonlat2utm(lon, lat, zone = 18) # we need to set the zone for this task!
angleUTM <- 180 / pi * atan(coef(lm(northing ~ easting, data = UTM))[2])
mapCoordinateSystem(lonR, latR, 500, angleUTM, col = 3)
legend("topright",
    lwd = 1, col = 2:3, bg = "white", title = "Axis Rotation Angle",
    legend = c(
        sprintf("geod: %.1f deg", angle),
        sprintf("utm:  %.1f deg", angleUTM)
    )
)

# }