Skip to contents

Make a Digital Filter

Source: R/misc.R
makeFilter.Rd

The results can be used in two different ways. CASE 1: for filtering, using filter() or convolve() or (for the asKernal=TRUE case) using kernapply(). For the Blackman-Harris filter, the half-power frequency is at 1/m cycles per time unit, as shown in the “Examples” section. When using filter() or kernapply() with these filters, use circular=TRUE. CASE 2: for windowing, if normalize is set to FALSE, as for example in computing a Welch spectral estimate.

Usage

makeFilter(
  type = c("blackman-harris", "rectangular", "hamming", "hann"),
  m,
  normalize = TRUE,
  asKernel = TRUE
)

Arguments

type

a string indicating the type of filter to use. (See Harris (1978) for a comparison of these and similar filters.) The choices for the present function are as follows.

  • "blackman-harris" yields a modified raised-cosine filter designated as "4-Term (-92 dB) Blackman-Harris" by Harris (1978; coefficients given in the table on page 65). This is also called "minimum 4-sample Blackman Harris" by that author, in his Table 1.

  • "rectangular" for a flat filter. (This is just for convenience. Note that kernel("daniell",....) gives the same result, in kernel form.)

  • "hamming" for a raised-cosine filter designed by Hamming. The mathematical form is a-(1-a)*cos(2*pi*i/(m-1)) where a is 0.54 and i is seq(0,m-1).

  • "hann" for a cosine filter that tapers to zero at the ends, i.e. of the same mathematical form as "hamming", but with a equal to 0.5.

m

length of filter.

normalize

logical value indicating whether to return numbers that sum to 1. This is TRUE by default, which is useful if the purpose is to lowpass filter a timeseries without altering power in the pass-band. However, normalize=FALSE is the right choice if the purpose is to window a timeseries, e.g. in computing a spectral estimate using Welch's method (see pwelch()).

asKernel

boolean, set to TRUE to get a smoothing kernel for the return value.

Value

If asKernel is FALSE, this returns a vector of filter coefficients, symmetric about the midpoint. The vector will sum to 1 if normalize=TRUE (i.e. by default). The return value may be used with filter(), which should be provided with argument circular=TRUE to avoid phase offsets. If asKernel is TRUE and if normalize is FALSE, an error is reported. On the other hand, if asKernel is TRUE and normalize is FALSE, then the return value is a smoothing kernel, which can be applied to a timeseries with kernapply(), whose bandwidth can be determined with bandwidth.kernel(), and which has both print and plot methods.

References

F. J. Harris, 1978. On the use of windows for harmonic analysis with the discrete Fourier Transform. Proceedings of the IEEE, 66(1), 51-83 (http://web.mit.edu/xiphmont/Public/windows.pdf.)

Author

Dan Kelley

Examples

library(oce)

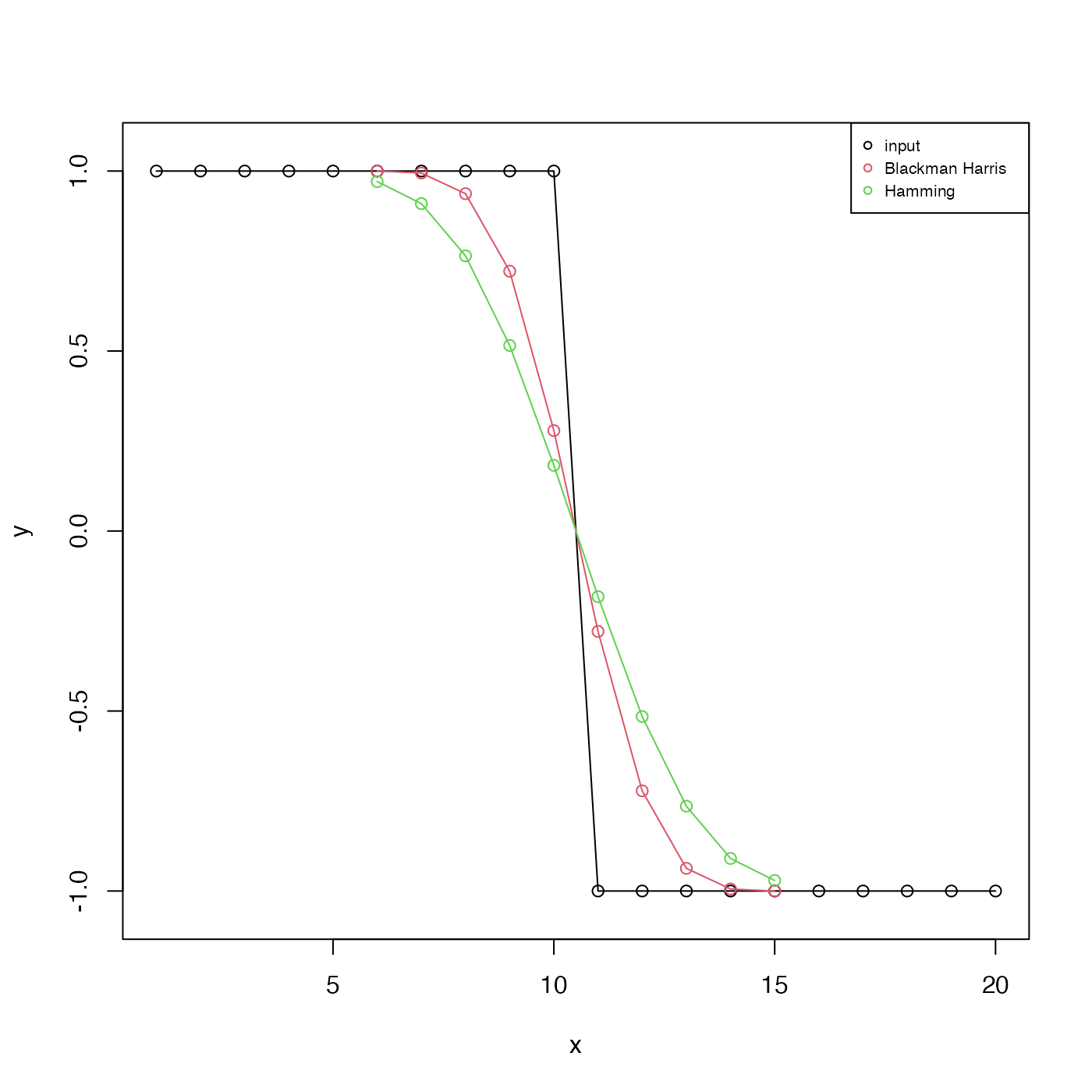
# Demonstrate step-function response
y <- c(rep(1, 10), rep(-1, 10))
x <- seq_along(y)
plot(x, y, type = "o", ylim = c(-1.05, 1.05))
BH <- makeFilter("blackman-harris", 11, asKernel = FALSE)
H <- makeFilter("hamming", 11, asKernel = FALSE)
yBH <- stats::filter(y, BH)
lines(x, yBH, type = "o", col = 2)
yH <- stats::filter(y, H)
lines(x, yH, type = "o", col = 3)
grid()
legend("topright",
    col = 1:3, bg = "white",
    legend = c("input", "Blackman Harris", "Hamming")
)