What is the optimal angle for a hammer throw?
Introduction
According to Reference 1, the best angle for hammer throw is approximately 44\(^\circ\), but athletes prefer to throw nearer 42\(^\circ\). My goal here is to see whether the former matches what I might expect from simple physics, and whether the latter imposes significant burden on athletes.
Theory
Newtonian mechanics will be assumed, with forces of (quadratic) air friction and the acceleration due to gravity being considered. This yields governing equations
\[m \frac{du}{dt} = - \frac{1}{2}\rho C_D A u U\]and
\[m \frac{dw}{dt} = -mg - \frac{1}{2}\rho C_D A w U\]Here, \(u\) and \(w\) are velocity components in the horizontal directions, \(U\) is the speed computed from these components, \(\rho\) is air density (here taken as 1.3 kg/m\(^3\)), \(C_D\) is drag coefficient (here taken as \(0.47\), a value commonly used for spheres; see Reference 2), and \(g\) is the acceleration due to gravity (here taken as 9.8 m/s\(^2\)).
The ball properties are mass \(m\) (7.26kg for males and 4kg for females) and plan area \(\pi R^2\) (with \(2R\) being 0.110m for males and 0.085m for females).
The initial condition was set in terms of throw speed \(U\) and release angle \(\theta\). It is assumed that the launch height is \(h_0=1.7\)m. The motion is tracked until vertical coordinate \(z\) reaches 0, i.e. ground level.
The computations are done using the lsoda function in the deSolve R
package. This is a well-regarded solver that automatically adjusts step size as
needed to attain a specified accuracy. I use it mainly for familiarity, and am
here not needing it’s hallmark advantage of handling mathematically “stiff”
problems well.
Procedure
As a base case, I will use the gold-medal results from the 2024 Olympics, according to Reference 3, i.e.
- Camryn Rogers (Canada) female Gold Medal 76.97 m.
- Ethan Katzberg (Canada) male Gold Medal 84.12 m.
The work has two main steps.
First, using fragments of the R code given below, I adjusted throwing speed $U$ through a series of trials in each of which the optimal angle was found, along with the distance achieved. This could have been done with optimization but I did it manually to explore the state space.
This work provided optimal angles at a speed that ought to be similar to that of the Olympic event. (The governing equations are nonlinear, so it is important to get speed in the right range.)
Second, I computed the speed increase that would be required if the athletes used a release angle of 42\(^\circ\), which is preferred by athletes, according to Reference 1.
Results
The output from the R code, i.e.
- male: with U = 28.801 m/s, the optimal angle of 44.19\(^\circ\) yields distance 84.12 m
- female: with U = 27.520 m/s, the optimal angle of 44.03\(^\circ\) yields distance 76.97 m
indicates that the optimal angle is 44.26\(^\circ\) for the male case and 44.03\(^\circ\) for the female case. These are consistent with Reference 2.
However, the speed increases required to achieve the same distances with the apparently preferred angle of 42\(^\circ\) is very slight, about 4 cm/s or a 0.15 percent increase, as indicated by the following output from the R code.
- male: with angle = 42.00\(^\circ\), using U = 28.845 m/s yields distance-observed = 0.010 m NOTE: this is a speed increase of 0.044 m/s (i.e. 0.15%)
- female: with angle = 42.00\(^\circ\), using U = 27.561 m/s yields distance-observed = 0.010 m NOTE: this is a speed increase of 0.041 m/s (i.e. 0.15%)
Below is a sample simulation (created in the last few lines of the R code shown at the end of this blog posting).
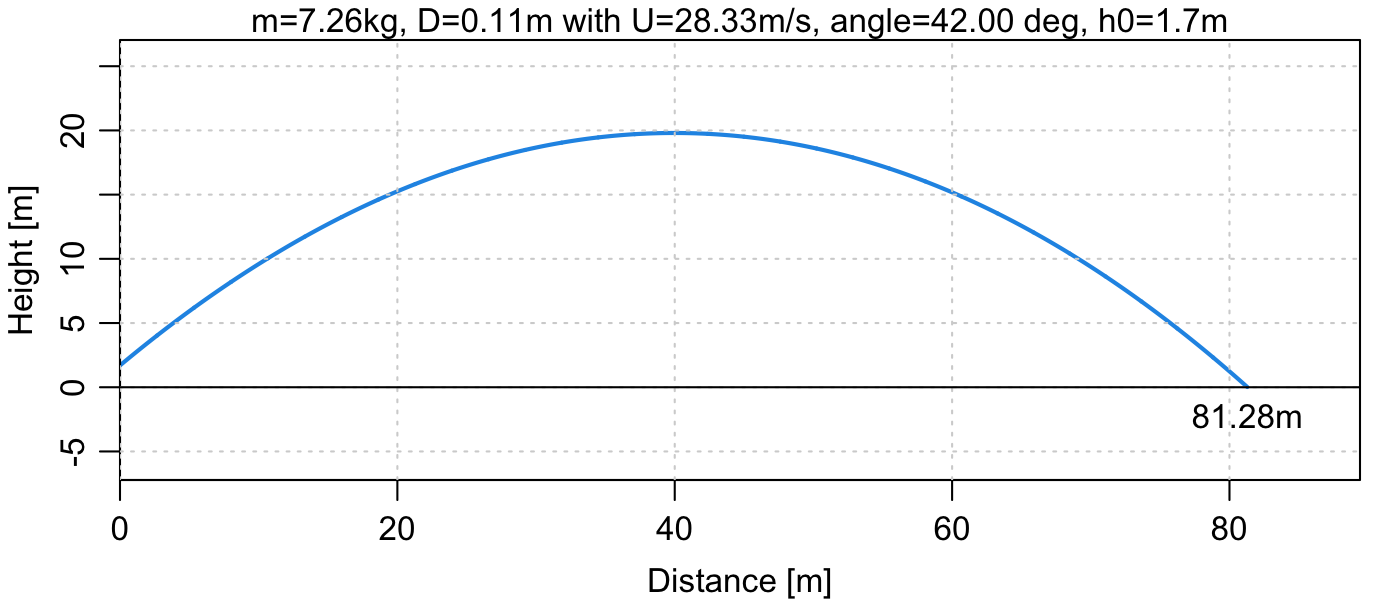
Conclusions
- The suggestion, in Reference 1, of an optimal angle of approximately 44\(^\circ\) matches the present findings.
- If an angle of 42\(^\circ\) is chosen instead, the release speed needs to be increased by about 4 cm/s (0.15 percent), which does not seem to be significant, if this shallower angle “feels” more comfortable.
To answer the question of the title, the optimal angle is approximately 44\(^\circ\), but lowering this to 42\(^\circ\), as is reportedly the custom, exacts a very low cost (a mere 0.15 percent increase in release velocity).
References
- Castaldi, Gian Mario, Riccardo Borzuola, Valentina Camomilla, Elena Bergamini, Giuseppe Vannozzi, and Andrea Macaluso. “Biomechanics of the Hammer Throw: Narrative Review.” Frontiers in Sports and Active Living 4 (March 31, 2022): 853536. https://doi.org/10.3389/fspor.2022.853536.
- https://en.wikipedia.org/wiki/Drag_coefficient
- https://olympics.com/en/paris-2024/results/athletics/men-s-hammer-throw/fnl-000100
R code for the computation
library(deSolve)
throw <- function(angle, U, h0 = 1.7, m = 4, D = 85e-3, plot = FALSE) {
func <- function(t, y, parms) {
A <- parms$A
m <- parms$m
CD <- parms$CD
rho <- parms$rho
g <- parms$g
u <- y[3]
w <- y[4]
U <- sqrt(u^2 + w^2)
dxdt <- u
dzdt <- w
dudt <- -0.5 * rho * CD * u * U * A / m
dwdt <- -0.5 * rho * CD * w * U * A / m - g
res <- c(dxdt, dzdt, dudt, dwdt)
list(res)
}
times <- seq(0, 5, length.out = 5000)
theta <- angle * pi / 180
u <- U * cos(theta)
w <- U * sin(theta)
y <- c(0, h0, u, w)
# CD is from https://en.wikipedia.org/wiki/Drag_coefficient
parms <- list(g = 9.8, rho = 1.3, CD = 0.47, m = m, A = pi * (D / 2)^2)
s <- lsoda(y = y, times = times, func = func, parms)
inair <- s[, 3] >= 0
s <- s[inair, ]
maxDistance <- max(s[, 2])
if (plot) {
par(mar = c(3, 3, 1, 1), mgp = c(2, 0.7, 0))
plot(s[, 2], s[, 3],
xlim = c(0, 1.1 * maxDistance),
type = "l", asp = 1,
lwd = 2, col = 4,
xaxs = "i", xlab = "Distance [m]", ylab = "Height [m]"
)
grid()
abline(h = 0)
text(maxDistance, 0, labels = sprintf("%.2fm", maxDistance), pos = 1)
mtext(sprintf("m=%.2fkg, D=%.2fm with U=%.2fm/s, angle=%.2f deg, h0=%.1fm", m, D, U, angle, h0))
}
maxDistance
}
# Find best angle for given speed, with the latter determined manually by
# running throw() with a series of U values, adjusting until the maximal
# distance matched the Olympic results to the published accuracy.
distance <- list(female = 76.97, male = 84.12)
for (gender in c("male", "female")) {
U <- list(female = 27.52, male = 28.801)[[gender]]
m <- list(female = 4, male = 7.26)[[gender]]
D <- list(female = 85e-3, male = 110e-3)[[gender]]
o <- optimize(\(angle) throw(angle, U, m = m, D = D), c(20, 60), maximum = TRUE)
cat(sprintf(
"* %s: with U = %.3f m/s, the optimal angle of %.2f deg yields distance %.2f m\n",
gender, U, o$maximum, o$objective
))
# Find speed to give recorded distance, at the assumed angle of 42 deg
angle <- 42
o <- optimize(\(U) abs(throw(angle, U, m = m, D = D) - distance[[gender]]),
c(10, 100),
maximum = FALSE
)
pc <- function(a, b) round(100 * (a - b) / b, 2)
cat(sprintf(
"* %s: with angle = %.2f deg, using U = %.3f m/s yields distance-observed = %.3f m\n",
gender, angle, o$minimum, o$objective
))
cat(
sprintf(
" NOTE: this is a speed increase of %.3f m/s (i.e. %.2f%%)\n",
o$minimum - U, pc(o$minimum, U)
)
)
}
# Draw a sample illustration of a trajectory (the male test case).
png("2024-08-07-hammer-throw.png", unit = "in", width = 7, height = 3, res = 200)
throw(angle = 42, U = 28.333, m = 7.26, D = 110e-3, plot = TRUE)
dev.off()