Valentines-day full moon

A wise person told me that it will be a full moon on the upcoming Valentine’s Day, but that it will be a long time until another one. I decided to check this with astronomical calculation, using the moonAngle() function of the oce package.

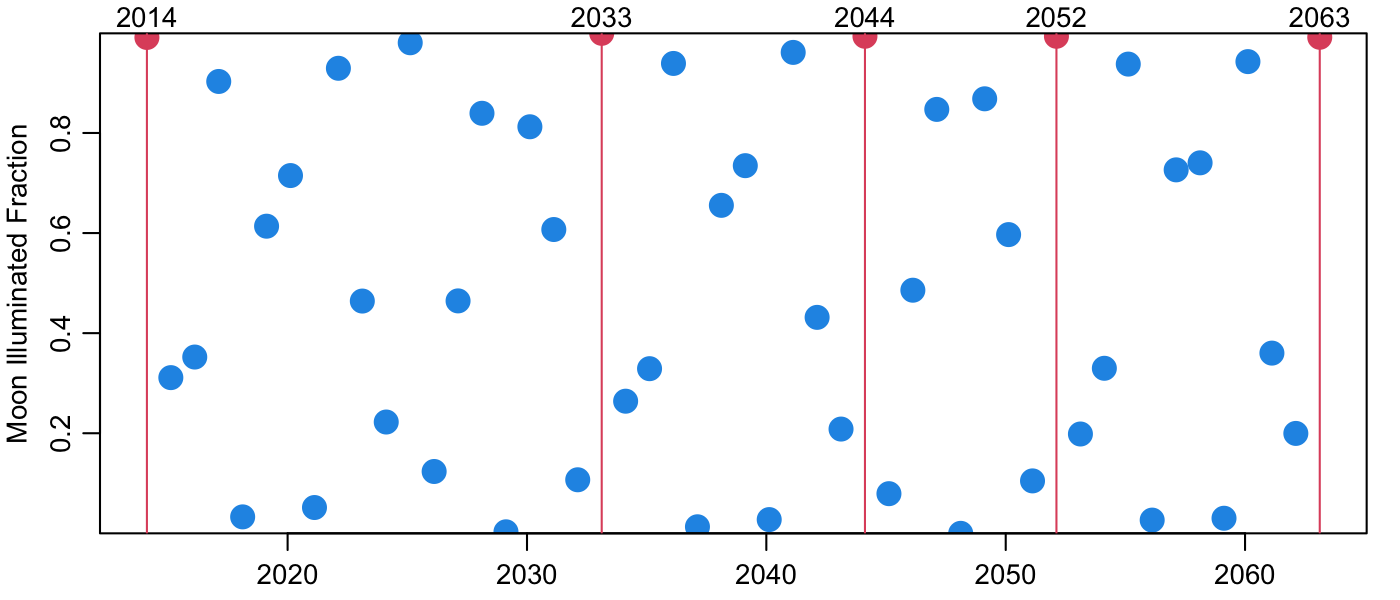
If you study the code at the bottom of the listing, you’ll see that I am computing the illuminated fraction of the moon for Valentine’s Days in the next few decades. If that fraction exceeds 99 percent, I call it a win, and colourize the dot red!

From the results we may infer a universal truth: buy candy now.

Code

library(oce)
times <- seq(as.POSIXct("2014-02-14", tz = "UTC"), length.out = 50, by = "year")
fraction <- moonAngle(times, longitude = -63, latitude = 43)$illuminatedFraction
full <- fraction > 0.99
timesFull <- times[full]
if (!interactive()) {
    png("2014-02-13-valentine-moon.png",
        unit = "in", res = 200,
        width = 7, height = 3, pointsize = 10
    )
}
par(mar = c(2, 3, 1, 1), mgp = c(2, 0.7, 0))
plot(times, fraction,
    yaxs = "i",
    xlab = "Year", ylab = "Moon Illuminated Fraction",
    col = ifelse(full, 2, 4), pch = 16, cex = 2
)
abline(v = timesFull, col = 2)
mtext(side = 3, at = timesFull, format(timesFull, "%Y"))