Introduction

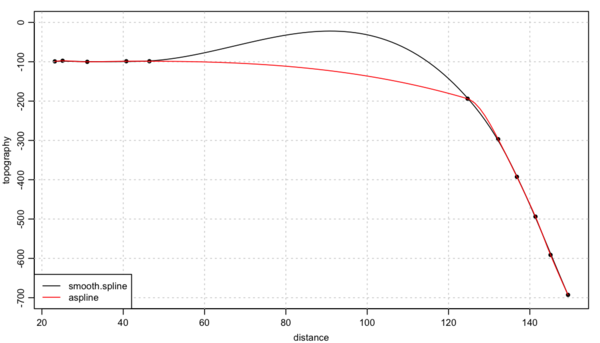
An interesting paper (Smith and Wessel, 1990) points out a weakness in using splines in cases with data gaps. Their illustration of the problem with isobaths was particularly compelling. I cannot reproduce their Fig 1b here, owing to copyright problems, but I digitized the data so I could test two R functions for splines. Readers can follow along with the code given in this post.

Methods

The first step is to load the data. (Ignore the extra digits, which simply result from naive copying of digitized values. I suppose the error is of order 2 percent or so, given the scanning of the diagram and my ability to position the pointer on my computer screen.)

1
2
3
4
5
6
distance <- c(23.17400, 25.09559, 31.15092, 40.75568,
              46.42938, 124.68628, 132.20556, 136.81277,
              141.37564, 145.08263, 149.38977)
topography <- c(-98.99976, -97.44730, -100.15198, -98.66016,
                -98.66016, -193.94266, -296.89045, -392.63991,
                -493.85330, -591.21586, -692.82951)

Next, plot the data.

1
2
3
4
if (!interactive()) png("splines.png", width=7, height=4, unit="in", res=150, pointsize=8)
par(mar=c(3, 3, 1, 1), mgp=c(2, 0.7, 0))
plot(distance, topography, ylim=c(-700, 0), pch=16)
grid()

Now, set up a grid, and show the results of smooth.spline().

1
2
3
4
d <- seq(min(distance), max(distance), length.out=100)
s <- smooth.spline(topography ~ distance)
ps <- predict(s, d)
lines(ps$x, ps$y)

Now, load the Akima package to get aspline(), which presumably stems from Akima (1970).

1
2
3
library(akima)
akima <- aspline(distance, topography, d)
lines(akima$x, akima$y, col='red')

Finally, draw a legend and finish up.

1
2
3
4
legend("bottomleft", lwd=par('lwd'), bg='white',
       col=c("black", "red"),
       legend=c("smooth.spline", "aspline"))
if (!interactive()) dev.off()

Results

At least on this problem, aspline() does a much better job than smooth.spline().

Citations

W. H. F. Smith and P. Wessel, 1990. Gridding with continuous curvature splines in tension. Geophysics, 55(3): 293-305.

Hiroshi Akima, 1970. A new method of interpolation and smooth curve fitting based on local procedures. Journal of the Association for Computing Machinery, 17(4): 589-602.