Introduction

Error propagation can be a fair bit of work with a calculator, but it’s easy with R. Just use R in repeated calculation with perturbed quantities, and inspect the range of results. Two methods are shown below for inspecting the range: sd() and quantile(), the latter using the fact that area under a normal distribution is 0.68 when calculated between -1 and 1 standard deviation.

Tests

Case 1: scale factor

In this case, the answer is simple. If A has uncertainty equal to 0.1, then 10A has uncertainty 1.0.

1
2
3
4
5
6
7
8
9
10
11
12
13
set.seed(123)

n <- 500
result <- vector("double", n)
A <- 1
Au <- 0.1 # uncertainty in A
for (i in 1:n) {
    Ap <- A + Au * rnorm(n=1)
    result[i] = 10 * Ap
}
D <- 0.5 * (1 - 0.68)
r <- quantile(result, probs=c(D, 1-D))
cat("value:", mean(result), "uncertainty:", sd(result), " range:", r[1], "to", r[2], "\n")

## value: 10.03 uncertainty: 0.9728  range: 9.047 to 11.02

1
hist(result)

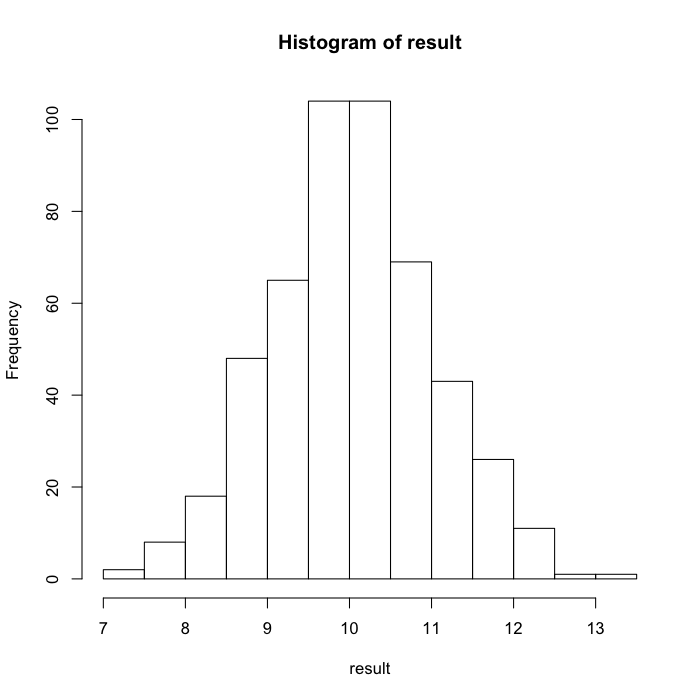
The graph indicates that the values are symmetric, which makes sense for a linear operation.

Case 2: squaring

Here, we expect an uncertainty of 20 percent.

1
2
3
4
5
6
7
8
9
10
11
12
set.seed(123)
n <- 500
result <- vector("double", n)
A <- 1
Au <- 0.1 # uncertainty in A
for (i in 1:n) {
    Ap <- A + Au * rnorm(n=1)
    result[i] = Ap^2
}
D <- 0.5 * (1 - 0.68)
r <- quantile(result, probs=c(D, 1-D))
cat("value:", mean(result), "uncertainty:", sd(result), " range:", r[1], "to", r[2], "\n")

## value: 1.016 uncertainty: 0.1965  range: 0.8184 to 1.213

1
hist(result)

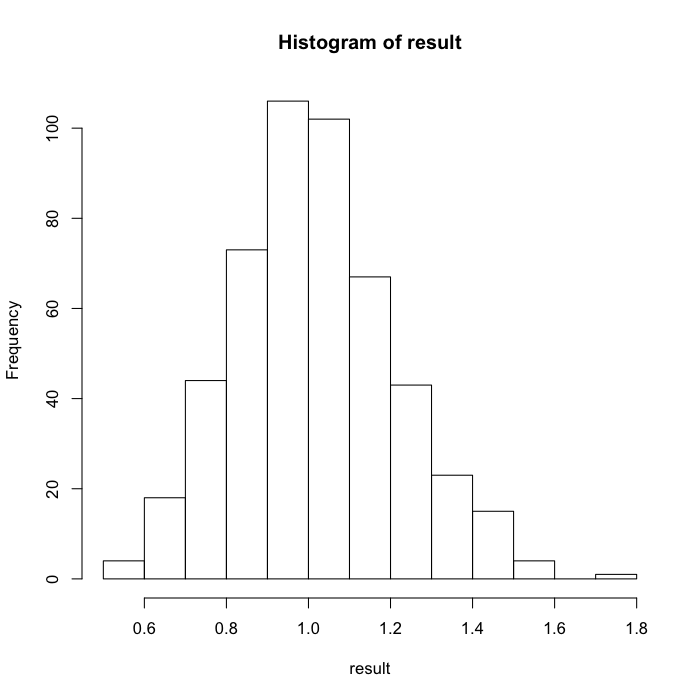
Case 3: a nonlinear function

Here, we have a hyperbolic tangent, so the expected error bar will be trickier analytically, but of course the R method remains simple. (Note that the uncertainty is increased to ensure a nonlinear range of hyperbolic tangent.)

1
2
3
4
5
6
7
8
9
10
11
12
set.seed(123)
n <- 500
result <- vector("double", n)
A <- 1
Au <- 0.5 # uncertainty in A
for (i in 1:n) {
    Ap <- A + Au * rnorm(n=1)
    result[i] = tanh(Ap)
}
D <- 0.5 * (1 - 0.68)
r <- quantile(result, probs=c(D, 1-D))
cat("value:", mean(result), "uncertainty:", sd(result), " range:", r[1], "to", r[2], "\n")

## value: 0.7009 uncertainty: 0.233  range: 0.4803 to 0.9065

1
hist(result)

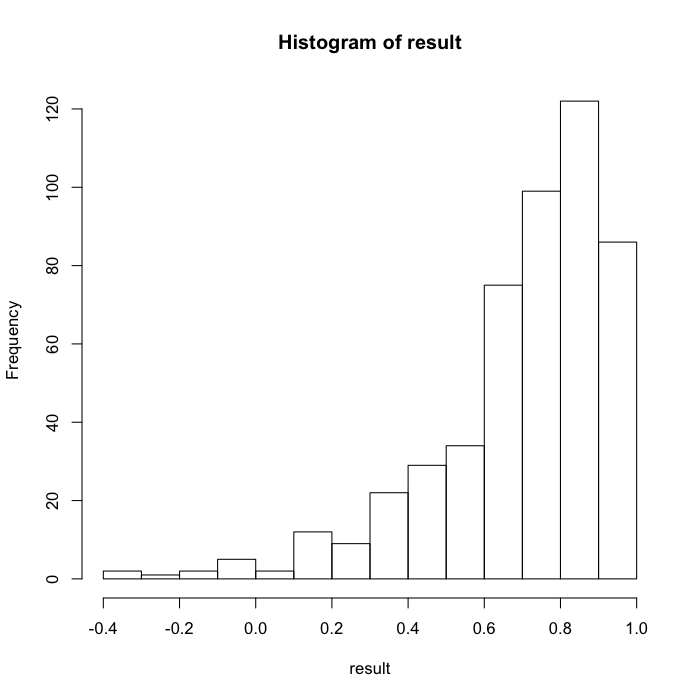
Conclusions

The computation is a simple matter of looping over a perturbed calculation. Here, gaussian errors are assumed, but other distributions could be used (e.g. quantities like kinetic energy that cannot be distributed in a Gaussian manner).

Further work

1. How large should n be, to get results to some desired resolution?

2. If the function is highly nonlinear, perhaps the mean(result) should be replaced by median(result), or something.

Resources

• R source code: 2014-03-05-error-bars-in-r.R